Survival Analysis of Hospitalized Very Low Birth Weight Infant Mortality in Taiwan
Chialin Chang, Wei-Chen Chen and Michael McAleer
DOI: 10.21767/2471-9927.10005
Chialin Chang1*, Wei-Chen Chen2,Michael McAleer3,4
1Department of Applied Economics, Department of Finance Economics, National Chung Hsing University, Taiwan
2Department of Applied Economics, National Chung Hsing University, Taiwan
3Department of Quantitative Finance, National Tsing Hua University, Taiwan
4Econometric Institute Erasmus, School of Economics, Erasmus University Rotterdam, The Netherlands
- *Corresponding Author:
- Chialin Chang
Department of Applied Economics
Department of Finance Economics
National Chung Hsing University, Taiwan
E-mail: jialin.chang.nchu@gmail.com
Tel: 88635715131
Received Date: August, 25 2015; Accepted Date: September, 25 2015; Published Date: October 15, 2015
Citation: Chang C, Chen WC, Michael McAleer. Survival Analysis of Hospitalized Very Low Birth Weight Infant Mortality in Taiwan. J Health MedEcon. 2015, 1:1.
Abstract
This paper examines the determinants of hospitalized very low birth weight infant (or neonatal) mortality using the Taiwan National Health Insurance Research database from 1997 to 2009. After infants are discharged from hospital, it is not possible to track their mortality, so the Cox proportional hazard model is used to analyze the very low birth weight infant mortality rate. In order to clarify treatment responsibility and to avoid selective referral effects, we use the number of infants treated in the preceding five years to observe the effect of a physician’s and hospital’s medical experience on the mortality rate of hospitalized minimal birth weight infants. The empirical results show that, given disease control variables, a higher infant weight, higher quality hospitals, increased hospital medical experience, and higher investment in pediatrics can reduce the mortality rate significantly. However, an increased physician’s medical experience does not seem to influence significantly the very low birth weight infant mortality rate.
Keywords
Very low birth weight; Neonatal mortality; Statistical analysis; Cox proportional hazard model; Selective referral; Taiwan National Health Insurance Scheme
Introduction
The survival of newborns (or infants) is widely known to depend on innate genetic factors, the mother’s previous medical history, the mother’s health condition during pregnancy, hospital of birth, postpartum medical conditions, and environmental health. Therefore, the survival rate of infants can be a direct measure of the health of mothers and infants, as well as an indirect measure of medical technology and environmental health.
Based on the definition of the World Health Organization (WHO), very low birth weight (VLBW) refers to a birth weight of less than 1500 g. Infants with minimal birth weights frequently suffer from serious complications of respiratory distress syndrome, neonatal intraventricular hemorrhage, necrotizing enterocolitis, congenital heart disease, congenital malformations, and retinal disease. Minimal birth weight infants are subject to treatments in the neonatal intensive care unit or neonatal intermediate unit, the cost of which can be a heavy financial burden for families.
Before the introduction of the Taiwan National Health Insurance scheme in 1995, there was a heavy economic and financial burden on families that had minimal birth weight infants. After the commencement of the Taiwan National Health Insurance scheme, the economic and financial burden was lifted substantially for such families.
Treating infants is different from treating adult patients. Establishing neonatology and providing physicians with appropriate medical equipment to care for infants indicates that the hospital has suitable quality for infant medical care. Previous studies have found that the establishment of a Neonatal Intensive Care Unit (NICU) enhanced a hospital’s care-giving technology which, in turn, led to reduced deaths of infants and minimal birth weight infants. These studies also found positive correlations among the occurrence of minimal birth weight infants, the number of neonatologists, and the number of beds in the NICU [1-3]. In addition to the above effects, the amount of surgery performed can also affect the mortality rate. Much of the literature is based on the complex surgery of coronary artery bypass to explore the relationship between surgical volume and the mortality rate, and treats surgical volume as an indirect measure of physician and hospital medical care quality [4-6].
However, there may be an endogeneity problem in the surgical volume and medical treatment effect (that is, medical quality).
The literature examines the effect of medical quality on mortality using surgical volume as a proxy for the latent medical quality. There may be endogeneity in these models if, for example, high mortality patients choose better quality hospitals.
In this sense, a high surgical volume and lower mortality is not caused by the medical treatment quality (or learning effect) but is, in fact, caused by a Selective-Referral Pattern. Previous empirical studies have also found that, after controlling for patient disease severity, an individual hospital’s annual surgical volume on patient mortality becomes insignificant [6-10].
A physician’s or hospital treatment of minimal birth weight infants is referred to as the Patient (or Infant) Volume. Previous research related to minimal birth weight infants, low birth weight infants, or infant volume and medical care quality have all shown a lower mortality rate for hospitals with high infant volume or NICU, with the relationship holding even after controlling for whether an infant is referred [10-15].
On the patient (or infant) volume calculation, the literature uses the daily number of hospitalizations, average annual infant volume, or current annual infant volumes as proxy variables. The daily number of hospitalizations is defined as the number of days that infants are hospitalized within a given period. If hospital admissions were to be concentrated within a specific time period, there will be periods without admissions being counted as periods with admissions, thereby causing bias in inflated infant volume. Similarly, the average annual infant volume is affected by extreme values, and may not be able to describe the annual variations.
The current annual infant volume takes into account only infant volume in the current year, and not past experience. Hence, the infant volume is unable to reflect the overall experience of the physician and/or the hospital. Unlike previous studies, this paper uses the accumulated infant volume to observe the effect of a physician’s and hospital experience on the mortality rate of hospitalized minimal birth weight infants.
This paper uses detailed hospitalization expense files from 1996 to 2009 from the Taiwan National Health Insurance database to observe the number of deaths of hospitalized minimal birth weight infants. The annual accumulated infant volume is used to represent the experience of both the physician and the hospital. Linking this to the basic information data file, the hospital evaluation classification and the number of hospital beds are used as explanatory variables to explore whether the physician and hospital characteristics, and accumulated infant volume, can affect hospital medical quality for minimal birth weight infants, and have explanatory power for the mortality rate of minimal birth weight infants.
The remainder of the paper is organized as follows. Section 2 presents the compilation of the National Health Insurance database, file linking procedures, and variable definitions. Section 3 introduces the empirical model. Section 4 explains the empirical results, and Section 5 gives some conclusions and health policy suggestions.
Data and Variables
The paper provides a statistical analysis of survival rate of minimal birth weight infants hospitalized for the first time. In analyzing the factors affecting the minimal birth weight infant mortality, the most important variables are infant weight classification, hospital infant survival time, infant discharge status, a physician’s experience, hospital infant experience, hospital evaluation classification, and the number of hospital beds. The data are obtained from the Taiwan National Health Insurance database, which provides five sub-data files: (1) medical institution basic information file (HOSB); (2) medical institution hospital bed master file (BED); (3) medical personnel basic information file (PER); (4) exclusive doctor certificate master file (DOC); and (5) detailed hospitalization expense file (DD).
As the National Health Insurance database does not allow an applicant to access an external database, it is not possible to determine an infant’s survival time after discharge.1 According to the hospitalization medical service point list media reporting format and form completion instruction, as provided by the website of the Taiwan National Health Insurance Administration, Ministry of Health and Welfare, Executive Yuan, the transfer code records the infant discharge condition noted as alive or deceased.2 This variable is noted in the 23rd column of the detailed hospitalization expense file in the National Health Insurance database, and the information for this field is required.
Although an infant’s survival time after discharge is unknown, the survival status at discharge is available. In addition, to clarify the accountability of the medical treatment and to avoid the effect of selective referral pattern (which indicates an infant’s referral to a physician or hospital with superior medical treatment quality), this paper eliminates data on minimal birth weight infants who are referred immediately after birth.
From the disease code of the International Statistical Classification of Diseases, revision nine (ICD9), which is recorded in the column of the diagnostic code of the detailed hospitalization expense file list (DD), we have the weight classification of every hospitalized infant (Table 1) for the selection of an infant’s International Statistical Classification of Diseases). The disease classification code divides weights into groups of under 500 g, 500 g to 749 g, 750 g to 999 g, 1000 g to 1249 g, and 1250 g to 1499 g. This paper uses data that are based on infants who are hospitalized immediately after birth, and whose disease code is recorded in the first column of Table 1.
Table 1: International Statistical Classification of Diseases and Related Health Problems, ICD.
| ICD Code | Disease description |
|---|---|
| 76401 | Light-for-dates without mention of fetal malnutrition, less than 500g |
| 76402 | Light-for-dates without mention of fetal malnutrition, 500-749g |
| 76403 | Light-for-dates without mention of fetal malnutrition, 750-999g |
| 76404 | Light-for-dates without mention of fetal malnutrition, 1000g-1249g |
| 76405 | Light-for-dates without mention of fetal malnutrition, 1250g-1499g |
| 76411 | Light-for-dates with signs of fetal malnutrition, less than 500g |
| 76412 | Light-for-dates with signs of fetal malnutrition,500-749g |
| 76413 | Light-for-dates with signs of fetal malnutrition, 750-999g |
| 76414 | Light-for-dates with signs of fetal malnutrition, 1000-1249g |
| 76415 | Light-for-dates with signs of fetal malnutrition, 1250-1499g |
| 76421 | Fetal malnutrition without mention “light-for-dates”, less than 500g |
| 76422 | Fetal malnutrition without mention “light-for-dates”,500-749g |
| 76423 | Fetal malnutrition without mention “light-for-dates”, 750-999g |
| 76424 | Fetal malnutrition without mention “light-for-dates”, 1000-1249g |
| 76425 | Fetal malnutrition without mention “light-for-dates”, 1250-1499g |
| 76491 | Fetal growth retardation, unspecified, less than 500g |
| 76492 | Fetal growth retardation, unspecified,500-749g |
| 76493 | Fetal growth retardation, unspecified, 750-999g |
| 76494 | Fetal growth retardation, unspecified, 1000-1249g |
| 76495 | Fetal growth retardation, unspecified,1250-1499g |
| 76501 | Extreme immaturity, less than 500g |
| 76502 | Extreme immaturity,500-749g |
| 76503 | Extreme immaturity,750-999g |
| 76504 | Extreme immaturity,1000-1249g |
| 76505 | Extreme immaturity,1250-1499g |
| 76511 | Other preterm immaturity, less than 500g |
| 76512 | Other preterm immaturity,500-749g |
| 76513 | Other preterm immaturity,750-999g |
| 76514 | Other preterm immaturity,1000-1249g |
| 76515 | Other preterm immaturity, 1250-1499g |
According to the hospitalization medical service point list media reporting format and form completion instruction of the National Health Insurance Administration, the detailed hospitalization expense file list (DD) and recorded main surgery (process) are optional rather than required.3 Therefore, not every infant has documented information for this field. Thus, this paper controls an infant’s disease severity based on a diagnostic code instead of a main surgery (process) code. In order to clarify the accountability of an infant’s medical treatment effect, only minimal birth weight infants who are cared for by only one physician from admission to discharge are included in the study.
From the detailed hospitalization expense file (DD), we have the codes of physicians and medical institutions for infants. Furthermore, from the medical personnel basic information file (PER) and exclusive doctor certificate master file (DOC), we can link this information to a physician’s gender, DOB, and certificate issue date. Furthermore, from the medical institution basic information file (HOSB) and the medical institution hospital beds master file (BED), we can link the above to hospital ownership, classification level, and the number of hospital beds.
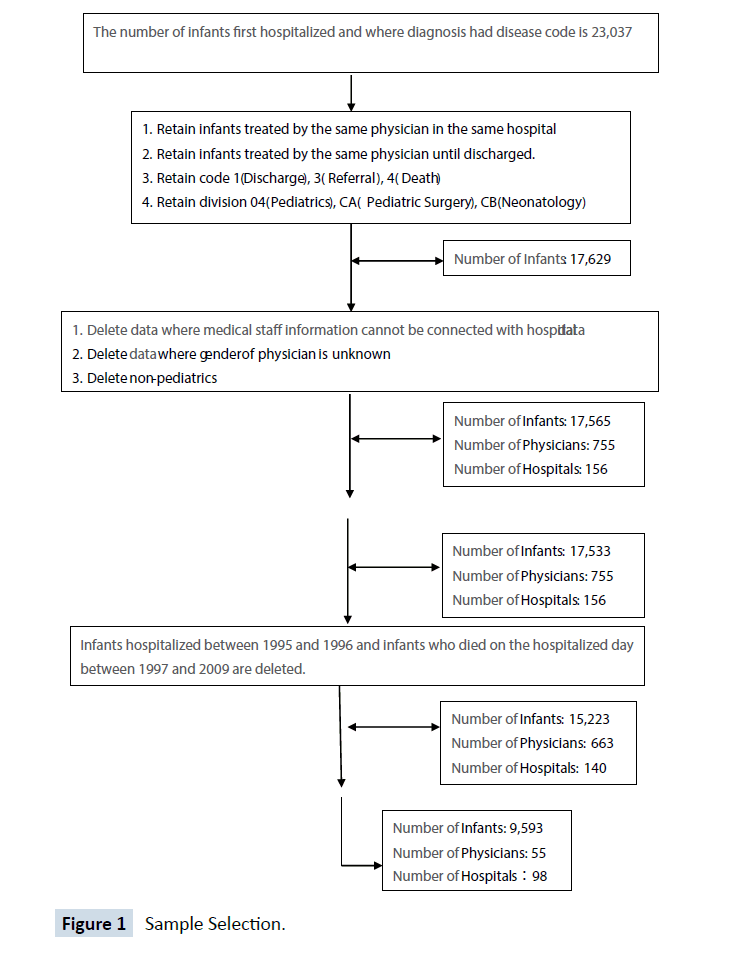
During compilation of the above sub-databases, phenomena such as unknown infant gender, infants treated by more than one physician, death on the day of birth (treated as stillbirth), referral on the first day of admission, unknown discharge status, seeking medical treatment from non-pediatricians, pediatric surgery, neonatology, physician’s unknown gender, a non-pediatric certified exclusive physician, and an inability to link a medical institution’s hospital beds to infants, all affect the number observations (refer to Diagram 1 for the sample screening process). In summary, if the file of hospital beds is not linked, there are 15,223 infants, 663 physicians, and 140 hospitals entering the final analysis whereas, if the file of hospital beds is linked, there are 9,593 infants, 455 physicians and 98 hospitals.
The dependent variable in this paper is survival time, the date of admission minus the date of discharge, excluding the day of discharge. Each sample observation also records the discharge status to determine whether an infant’s survival time is restricted data. Referral codes 1 (treatment and discharge) and 3 (transfer to outpatient treatment) are defined as discharge status alive, but the survival time after discharge is unknown, and hence is treated as restricted data. Referral code 4 (death) is defined as discharge status death, representing an event’s occurrence. The explanatory variables include infant’s characteristics (Zpatient), physician’s characteristics (Zprsn), and hospital characteristics (Zhosp), which are explained below and in Table 2.
Table 2: Variables.
| Dependent variable | Definition |
|---|---|
| Survival time | Discharge date minus admission date (excluding the day of discharge) |
| Discharge status | Death=1, Survival=0 |
| Independent variables | |
| Infant Characteristics (Zpatient) | |
| Weight between 1250g and 1499g | Weight between 1250g-1499g=1, others=0 |
| Weight between 1000g and 1249g | Weight between 1000g-1249g=1, others=0 |
| Weight between 750g and 999g | Weight between 750g-999g=1, others=0 |
| Weight between 500g and 749g | Weight between 500g-749g=1, others=0 |
| Weight less than 500g | Weight less than 500g=1, others=0 |
| Infant’s gender | Male=1, Female=0 |
| Respiratory Diseases (ICD9_CM 769-770) | Infants who have this disease=1 , others=0 |
| Fetal and neonatal intraventricular hemorrhage (ICD9_CM 772.1) | Infants who have this disease=1 , others=0 |
| Retinal disorder (ICD9_CM 362) | Infants who have this disease=1 , others=0 |
| Congenital Heart Disease ICD9_CM 745-746.85) | Infants who have this disease=1 , others=0 |
| Necrotizing enterocolitis in fetus or infant (ICD9_CM 777.5) | Infants who have this disease=1 , others=0 |
| Physician’s Characteristics (Zprsn) | |
| Physician’s experience (5 years) | Number of very low birth weight infants a physician has treated in the previous five years. |
| Physician’s gender | Male=1, Female=0 |
| Physician’s seniority | Seniority of physicians on the day infants are hospitalized (calculated by day) |
| Physician’s age | Ages of physicians on the day infants are hospitalized (calculated by day) |
| Hospital Characteristics (Zhosp) | |
| Hospital experience (5 years) | Number of very low birth weight infants the hospital has treated in the previous five years. |
| Medical center | Medical center=1, others=0 |
| Regional hospital | Regional hospital=1, others=0 |
| Ownership | Private hospital=1, others=0 |
| Medical center and private hospital | Medical center and private hospital=1, others=0 |
| Regional hospital and private hospital | Regional hospital and private hospital=1, others=0 |
| Medical center and public hospital | Medical center and public hospital =1, others=0 |
| Regional hospital and public hospital | Regional hospital and public hospital, others=0 |
| Number of acute infant intensive care beds | Number of acute infant intensive care beds that medical institutions owned for the year |
| Total number of beds | Total number of beds that medical institutions owned for the year |
Table 3 presents the sample descriptive statistics, and is given according to the order of Zpatient (infant’s characteristics), Zprsn (physician’s characteristics), and Zhosp (hospital characteristics). The mean infnat hospitalization is 49 days, maximum hospitalization is 779 days, and minimum hospitalization is one day. During the period of study, the number of deaths is 1,952 infants, which is about 2%. Infants with weights between 1250 g and 1499 g number 4,087, or about 43%; with weights between 1000 g and 1249 g number 2,658, or about 28%; with weights between 750 g and 999 g number 1,698, or about 18%; with weights between 500 g and 749 g number 1,014, or about 11%; and with weights of less than 500 g number 151, or about 2%.
Table 3: Descriptive Statistics.
| Variables | Obs. | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| Survival time | 9593 | 49.20 | 33.41 | 1 | 779 |
| Discharge status | 9593 | 0.20 | 0.40 | 0 | 1 |
| Infant Characteristics (Zpatient) | |||||
| Weight between 1250g and 1499g | 9593 | 0.43 | 0.49 | 0 | 1 |
| Weight between 1000 g and 1249 g | 9593 | 0.28 | 0.45 | 0 | 1 |
| Weight between 750g and 999g | 9593 | 0.18 | 0.38 | 0 | 1 |
| Weight between 500g and 749g | 9593 | 0.11 | 0.31 | 0 | 1 |
| Weight less than 500g | 9593 | 0.02 | 0.12 | 0 | 1 |
| Infant’s gender _Male | 6732 | 0.51 | 0.50 | 0 | 1 |
| Respiratory Diseases | 9593 | 0.63 | 0.48 | 0 | 1 |
| Fetal and neonatal intraventricular Hemorrhage | 9593 | 0.10 | 0.29 | 0 | 1 |
| Other retinal disorder | 9593 | 0.10 | 0.30 | 0 | 1 |
| Congenital Heart Disease | 9593 | 0.25 | 0.43 | 0 | 1 |
| Necrotizing enterocolitis in fetus or infant | 9593 | 0.04 | 0.19 | 0 | 1 |
| Physician’s Characteristics (Zprsn) | |||||
| Physician’s experience (5 years) | 9593 | 51.08 | 46.60 | 0 | 224 |
| Physician’s gender _Male | 9593 | 0.63 | 0.48 | 0 | 1 |
| Physician’s seniority | 9593 | 4114.28 | 2167.75 | 61 | 12191 |
| Physician’s age | 9593 | 15700.77 | 3165.38 | 9867 | 25910 |
| Hospital Characteristics (Zhosp) | |||||
| Hospital experience (5 years) | 9593 | 187.73 | 162.89 | 0 | 604 |
| Medical center | 9593 | 0.69 | 0.46 | 0 | 1 |
| Regional hospital | 9593 | 0.26 | 0.44 | 0 | 1 |
| Ownership _Private hospital | 9593 | 0.79 | 0.41 | 0 | 1 |
| Medical center and private hospital | 9593 | 0.51 | 0.50 | 0 | 1 |
| Regional hospital and private hospital | 9593 | 0.22 | 0.42 | 0 | 1 |
| Medical center and public hospital | 9593 | 0.17 | 0.38 | 0 | 1 |
| Regional hospital and public hospital | 9593 | 0.04 | 0.19 | 0 | 1 |
| Number of acute infant intensive care beds | 9593 | 28.69 | 36.84 | 0 | 119 |
| Total number of beds | 9593 | 1087.69 | 913.65 | 1 | 3689 |
Infants suffering from respiratory diseases number 6,083, representing approximately 63% of the sample observations; infnats suffering from neonatal intraventricular hemorrhage number 920, representing approximately 10% of the sample observations; infants suffering from retinal disease number 955, representing approximately 10% of the sample observations; infants suffering from congenital heart disease number 2,355, representing approximately 25% of the sample observations; and infants suffering from necrotizing enterocolitis number 378, representing approximately 4% of the sample observations. After linking to the hospital beds file, there are 3,444 infant boys and 3,288 infant girls in the paper card samples.
Infants treated by male physicians number 6,058, representing approximately 63% of the sample observations; and infants treated by female physicians number 3,535, representing approximately 37% of the sample observations. At the time of treatment, the mean physician seniority is 4,114 days and the mean age is 15,700 days. For physicians with five years of infant experience, the mean is 51 and the standard deviation is 46.
Infants staying in the medical center number 6,585, representing approximately 69% of the sample observations; infants staying in the regional hospital number 2,465, representing approximately 26% of the sample observations; infants staying in the district hospital number 543, representing approximately 5% of the sample observations; infants staying in private hospitals number 7,551, representing approximately 79% of the sample observations; infants staying in the medical center of private hospitals number 4,937, representing approximately 51% of the sample observations; infants staying in the medical center of public hospitals number 1,648, representing approximately 17% of the sample observations; infants staying in private regional hospitals number 2,124, representing approximately 22% of the sample observations; and infants staying in public regional hospitals number 341, representing approximately 4% of the sample observations.
For the sample period, the total number of hospital beds is 1,087, with a standard deviation of 913 beds. The mean acute newborn intensive care beds number 28, with a standard deviation of 36 beds. For hospitals with five years of infant experience, the mean is 187 infants with standard deviation of 162 infants.
Prior to September 2003, the National Health Insurance scheme used paper cards. The government required all patients to use their own health insurance cards, and hence did not allow infants to use their mother’s health insurance cards for medical treatment.
However, after September 2003, the National Health Insurance scheme switched to Integrated Circuit (IC) cards. Therefore, within the first 31 days of birth, infants could use their mother’s health insurance IC cards if hospitalization were needed immediately after birth.4 In short, before September 2003, an infant’s gender is indicated on the detailed hospitalization expense file, but only a mother’s gender is recorded after September 2003. Hence, this paper divides the samples into groups of paper cards, IC cards, and a mixed sample of paper and IC cards.
Empirical Model
In order to analyze the factors affecting the mortality rate of minimal birth weight infants, this paper uses the Cox proportional hazard model. Let T be the random variable of survival time. The cumulative distribution function of survival time is Pr (T≤t) =F(t), representing the cumulative probability of survival until time t. The survival function can be defined as Pr(T ≥ t) = 1− F(t) = S(t), representing the probability of survival over time t. The hazard function is defined as:
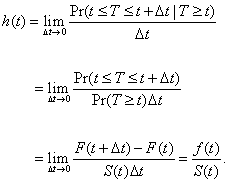 (1)
(1)
The hazard function represents the probability density function of an immediate event occurring under the condition that the given sample observation value can survive at least until time t, and can be solved from the following equation:
 (2)
(2)
The proportional hazard model is given in equation (3), which can be used for the analysis of the determinants affecting the probability of survival over time t:
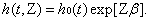 (3)
(3)
In equation (3), Z is the dependent variable, β is the unknown parameter to be estimated, and h0(t) is the baseline hazard function. Without any assumption on h0(t), the proportional hazard model is a semi-parametric model, which can be estimated by the likelihood method).
Under the assumption of a non-repetitive survival time for each observation (that is, without tied data), the likelihood function can be written as follows:
 (4)
(4)
where ci = 1 (uncensored) represents the sample event occurring during the observation period, ci = 0 (censored) represents no sample event occurring during the observation period, and R(ti) is the risk set, representing all the sample observations remaining alive until time ti . In equation (4), the sample observation value is one and is unable to provide any information when ci = 0. Hence, for ci = 1 and arranging the sample observations in ascending order based on the survival time, equation (4) can be rearranged as follows:
 (5)
(5)
In equation (5), k represents the number of survival times after arranging the order: for example, for a total of 10 infants, if an event occurred for seven people and the survival time is not repeated, then
k = 7; if the survival time is repeated for two infants and not the other five, then k = 6. In equation (5) t(i) represents the sorted survival time and R(t(i)) represents the risk set, which denotes all sample observations still surviving until time t(i). Hence, the risk set includes the censored sample. Taking logarithms of equation (5) leads to the following:
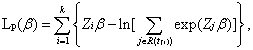 (6)
(6)
which may be optimized to obtain estimates of β as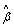 When the survival times of the sample observations are repeated
(tied), equation (6) no longer applies for estimation. Hence,
Breslow suggested the partial likelihood function in equation (7):
When the survival times of the sample observations are repeated
(tied), equation (6) no longer applies for estimation. Hence,
Breslow suggested the partial likelihood function in equation (7):
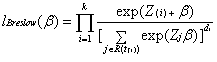
Efron (1977) suggested the partial likelihood function in equation (8):
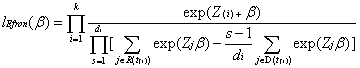 (8)
(8)
where K represents the number of sorted survival times, d,(i) denotes the number of sample observations when the survival
time is t(i)and the event occurred, and  represents
the sample set when the survival time D(t(i)) equals t(i)and the event occurred. For example, suppose the survival time for A and
B is three days and the event (death) occurs on the third day,
then
represents
the sample set when the survival time D(t(i)) equals t(i)and the event occurred. For example, suppose the survival time for A and
B is three days and the event (death) occurs on the third day,
then 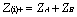 Therefore, the numerator in equations (7) and
(8) is
Therefore, the numerator in equations (7) and
(8) is 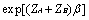 and di = 2. On the other hand, equations (7)
and (8) can revert to equation (5) if only one event occurs fork
survival times (that is,
and di = 2. On the other hand, equations (7)
and (8) can revert to equation (5) if only one event occurs fork
survival times (that is,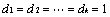 ).
).
The primary difference between Breslow and Efron for samples with the same survival times is in the setting of the denominator. Breslow gives the same weight to each sample observation with the same survival time if the event occurred, while Efron gives different weights. The Breslow estimating equation is given in equation (9) below:
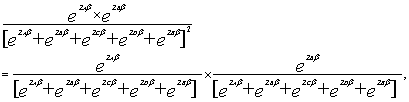 (9)
(9)
while the Efron estimating equation is given in equation (10):
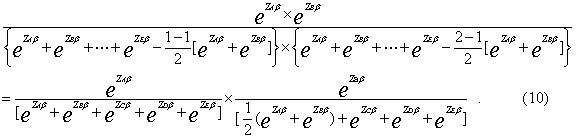
From equations (9) and (10), Efron gives weights of 1/2 to both the A and B observations with the same survival times, while Breslow gives both values a weight of one. As the denominator in equation (10) is smaller thatn that in (9), the likelihood value of the Efron estimator is greater than that of the Breslow estimator. Therefore, the greater is the number of observations with the same survival time, the larger will be the likelihood of Efron relative to that of Breslow. As there are observations with the same survival times in the data set, in order to have improved estimates, estimation will be based mainly on the Efron procedure.
The dependent variable in survival analysis is categorized according to the survival times when the event occurs, or when no event occurs, in which case the specific observation will be registered as a censored survival time. The proportional hazard model is different from the linear regression model where each explanatory variable can change the dependent variable separately. On the contrary, in a proportional hazard model, the effect of each explanatory variable depends on the hazard ratio.
Assume that we have already estimated the regression
parameter,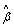 , and there is only one explanatory variable, for
example, gender, defined as follows:
, and there is only one explanatory variable, for
example, gender, defined as follows:

The definition of the hazard ratio is given in equation (11):
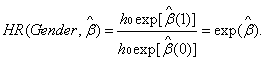 (11)
(11)
If 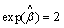 , the sudden infant mortality rate of females is twice
that of males. Notice that h0(t) in the numerator and denominator cancel each other, so that the sudden infant mortality is
proportional. As the proportional relationship does not change
over time, the model in equation (11) is called the proportional
hazard model.
, the sudden infant mortality rate of females is twice
that of males. Notice that h0(t) in the numerator and denominator cancel each other, so that the sudden infant mortality is
proportional. As the proportional relationship does not change
over time, the model in equation (11) is called the proportional
hazard model.
Similarly, if there exists a sequential explanatory variable, such as age (in years), then the hazard ratio is given in equation (12):
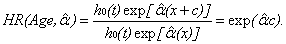 (12)
(12)
If exp(αˆc) = 1.2 , for every c years the age increases, the sudden infant mortality rate is 1.2 times that of the initial value, which is an increase of 20% in the sudden infant mortality rate. For further details on the definition and estimation of the Cox proportional hazard model, as well as the meaning of the hazard ratio see, for example, Hosmer [16].
This paper extends the Cox proportional hazard model, as follows:
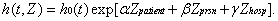 (13)
(13)
There are three types of dimensions of explanatory variables in the model in equation (13): Zpatient represents the infant’s characteristics, Zprsn represents the physician’s characteristics, and Zhosp represents the hospital characteristics. An infant’s characteristics include weight and disease category; a physician’s characteristics include gender, seniority, age, and infant experience; and hospital characteristics include the hospital infant experience, evaluation classification (medical center and regional hospital), ownership effect (private or public hospital), cross effect of evaluation classification and ownership (medical center and private hospital, regional and private hospital), number of acute infant intensive care beds, and the hospital’s total number of beds. As above, this paper adopts the Efron partial likelihood function for estimating the unknown parameters of the proportional hazard model.
As weight classification has a more stable relationship than the disease category control variable, in order to understand the determining factors of the mortality rate of minimal birth weight infants, this paper has four research model settings: (i) the basic model (without the disease control variables); (ii) the basic model with the disease control variables; (iii) the basic model with the number of hospital beds; and (iv) the basic model with the disease control variables and the number of hospital beds.
Empirical Results
Tables 4-7 show the results from Efron estimation, in which all the coefficient values are converted to hazard ratios. As described in Second 2 above, prior to September 2003, the Taiwan National Health Insurance scheme used paper cards. The government required all patients to use their own health insurance cards, and did not allow infants to access medical services using their mothers’ insurance cards. As of September 2003, the National Health Insurance scheme switched to IC cards, so that infants who required hospitalization immediately after birth could use their mother’s insurance cards to access medical services during their first 31 days. As the sample observations in this paper include both paper card and IC card data, the empirical results below will show the estimates for the paper card sample, IC card sample, and a mixed sample of paper and IC cards.
Table 4: Basic Model.
| Variables | IC+ Paper cards | Paper cards |
|---|---|---|
| Infant Characteristics (Zpatient) | ||
| Weight between 1250g and 1499g | 0.0285** (-36.44) | 0.0244** (-29.07) |
| Weight between 1000g and 1249g | 0.0674** (-29.56) | 0.0612** (-23.40) |
| Weight between 750g and 999g | 0.215** (-18.02) | 0.179** (-15.13) |
| Weight between 500g and 749g | 0.669** (-4.82) | 0.548** (-5.38) |
| Infant’s gender _Male | - | 1.406** (7.02) |
| Physician’s Characteristics (Zprsn) | ||
| Physician’s gender _Male | 1.023 (0.55) | 1.082 (1.48) |
| Physician’s seniority | 0.999** (-5.91) | 0.999** (-2.79) |
| Physician’s age | 1.001** (4.21) | 1.001* (2.44) |
| Physician’s experience (5 years) | 0.999* (-2.42) | 0.999** (-2.78) |
| Hospital Characteristics (Zhosp) | ||
| Medical center | 0.750** (-3.43) | 0.710** (-3.41) |
| Medical center and private hospital | 1.047 (0.74) | 0.993 (-0.08) |
| Regional hospital and private hospital | 1.037 (0.49) | 1.037 (0.42) |
| Hospital experience (5 years) | 0.999** (-6.36) | 0.999* (-2.15) |
| LR chi2 | 3683.2 | 2234.1 |
| Prob>chi2 | 0 | 0 |
| Observations | 15223 | 8677 |
Notes: 1. The coefficients of the independent variables have been transformed into the hazard ratio.
2.* significant at 5%; ** significant at 1%.
3. Numbers in parentheses are t-values.
Table 5: Basic Model and Disease Control Variable..
| Variables | IC+ Paper cards | Paper cards |
|---|---|---|
| Infant Characteristics (Zpatient) | ||
| Weight between 1250g and 1499g | 0.0294*** (-36.05) | 0.0246*** (-28.88) |
| Weight between 1000g and 1249g | 0.0726*** (-28.61) | 0.0650*** (-22.75) |
| Weight between 750g and 999g | 0.258*** (-15.74) | 0.207*** (-13.67) |
| Weight between 500g and 749g | 0.745*** (-3.50) | 0.586*** (-4.74) |
| Infant’s gender _Male | 1.339*** | |
| Physician’s Characteristics (Zprsn) | (5.99) | |
| Physician’s gender _Male | 1.082* (1.90) | 1.137** (2.41) |
| Physician’s seniority | 0.999*** (-6.77) | 0.999*** (-2.68) |
| Physician’s age | 1.001*** (3.91) | 1.001 (1.48) |
| Physician’s experience (5 years) | 0.999 (-0.66) | 0.999 (-1.02) |
| Hospital Characteristics (Zhosp) | ||
| Medical center | 0.870** (-2.35) | 0.811*** (-2.78) |
| Medical center and public hospital | 0.875** (-2.11) | 0.858* (-1.88) |
| Regional hospital and public hospital | 0.996 (-0.04) | 0.991 (-0.07) |
| Hospital experience (5 years) | 0.999*** (-4.91) | 1.000** (-2.01) |
| Disease | ||
| Respiratory Diseases | 1.060 (1.27) | 1.062 (1.02) |
| Fetal and neonatal intraventricular hemorrhage | 1.257*** (4.30) | 1.241*** (3.20) |
| Other retinal disorder | 0.0591*** (-16.22) | 0.0605*** (-12.99) |
| Congenital Heart Disease | 0.604*** (-10.69) | 0.644*** (-7.53) |
| Necrotizing enterocolitis in fetus or infant | 0.616*** (-4.92) | 0.678*** (-3.29) |
| LR chi2 | 4593.9 | 2791.8 |
| Prob>chi2 | 0 | 0 |
| Observations | 15223 | 8677 |
Notes: 1. The coefficients of the independent variables have been transformed into the hazard ratio.
2.* significant at 10%; ** significant at 5%; *** significant at 1%.
3. Numbers in parentheses are t-values.
Table 6: Basic Model and Disease Control Variable.
| Variables | IC+ Paper Cards | Paper card | ||
|---|---|---|---|---|
| Infant Characteristics (Zpatient) | [1] | [2] | [1] | [2] |
| Weight between 1250g and 1499g | 0.0272*** (-30.55) | 0.0271*** (-30.57) | 0.0267*** (-25.58) | 0.0268*** (-25.58) |
| Weight between 1000g and 1249g | 0.0667*** (-24.51) | 0.0665*** (-24.53) | 0.0665*** (-20.38) | 0.0666*** (-20.37) |
| Weight between 750g and 999g | 0.201*** (-15.35) | 0.200*** (-15.38) | 0.191*** (-12.93) | 0.191*** (-12.93) |
| Weight between 500g and 749g | 0.622*** (-4.64) | 0.621*** (-4.66) | 0.567*** (-4.50) | 0.568*** (-4.49) |
| Infant’s gender _Male | 1.447*** (6.91) | 1.446*** (6.91) | ||
| Physician’s Characteristics (Zprsn) | ||||
| Physician’s gender _Male | 1.064 (1.25) | 1.067 (1.29) | 1.141** (2.27) | 1.151** (2.39) |
| Physician’s seniority | 0.999*** (-4.43) | 0.999*** (-4.72) | 0.999 (-1.27) | 0.999 (-1.38) |
| Physician’s age | 1.001** (2.23) | 1.001** (2.40) | 1.001 (0.94) | 1.001 (0.90) |
| Physician’s experience (5 years) | 1.001 (0.34) | 1.001 (0.09) | 0.999 (-1.25) | 0.999 (-1.04) |
| Hospital Characteristics (Zhosp) | ||||
| Medical center | 0.584*** (-7.33) | 0.598*** (-7.20) | 0.622*** (-5.27) | 0.608*** (-5.90) |
| Medical center and public hospital | 1.004 (0.05) | 1.027 (0.36) | 1.034 (0.36) | 1.036 (0.38) |
| Regional hospital and public hospital | 0.963 (-0.32) | 0.950 (-0.44) | 0.843 (-1.26) | 0.843 (-1.26) |
| Hospital experience (5 years) | 0.999* (-1.74) | 0.999* (-1.66) | 0.999 (-0.68) | 0.999 (-1.01) |
| Bed | ||||
| Total number of beds | 1.001 (1.23) | 0.999 (-0.61) | ||
| Number of acute newborn intensive care beds | 1.001 (1.10) | 1.001 (0.77) | ||
| LR chi2 | 2526.3 | 2526 | 1806 | 1806.2 |
| Prob>chi2 | 0 | 0 | 0 | 0 |
| Observations | 9593 | 9593 | 6732 | 6732 |
Table 7: Basic Model and Control for Disease and the Number of Beds.
| Variables | IC+ Paper Cards | Paper card | ||
|---|---|---|---|---|
| Infant Characteristics (Zpatient) | [1] | [2] | [1] | [2] |
| Weight between 1250g and 1499g | 0.0277*** (-30.28) | 0.0276*** (-30.30) | 0.0273*** (-25.36) | 0.0272*** (-25.39) |
| Weight between 1000g and 1249g | 0.0707*** (-23.82) | 0.0704*** (-23.85) | 0.0706*** (-19.80) | 0.0705*** (-19.82) |
| Weight between 750g and 999g | 0.235*** (-13.71) | 0.235*** (-13.72) | 0.219*** (-11.73) | 0.221*** (-11.69) |
| Weight between 500g and 749g | 0.668*** (-3.91) | 0.666*** (-3.93) | 0.602*** (-4.00) | 0.602*** (-4.00) |
| Infant’s gender _Male | 1.357*** (5.70) | 1.356*** (5.68) | ||
| Physician’s Characteristics (Zprsn) | ||||
| Physician’s gender _Male | 1.132** (2.47) | 1.092* (1.74) | 1.175*** (2.75) | 1.149** (2.35) |
| Physician’s seniority | 1.000*** (-5.36) | 1.000*** (-5.16) | 1.000* (-1.78) | 1.000 (-1.26) |
| Physician’s age | 1.000** (2.18) | 1.000** (2.54) | 1.000 (0.78) | 1.000 (0.87) |
| Physician’s experience (5 years) | 1.001 (1.16) | 1.000 (0.34) | 1.000 (-0.05) | 1.000 (-0.44) |
| Hospital Characteristics (Zhosp) | ||||
| Medical center | 0.649*** (-5.81) | 0.677*** (-5.41) | 0.689*** (-4.08) | 0.709*** (-4.03) |
| Medical center and public hospital | 0.933 (-0.91) | 0.964 (-0.49) | 0.901 (-1.11) | 0.885 (-1.30) |
| Regional hospital and public hospital | 1.030 (0.25) | 1.022 (0.19) | 0.894 (-0.82) | 0.904 (-0.74) |
| Hospital experience (5 years) | 0.999 (-1.63) | 0.999 (-0.45) | 0.999 (-0.91) | 0.999 (-0.29) |
| Disease | ||||
| Respiratory Diseases | 1.122** (2.19) | 1.124** (2.23) | 1.095 (1.46) | 1.093 (1.43) |
| Fetal and neonatal intraventricular hemorrhage | 1.257*** (3.57) | 1.255*** (3.54) | 1.252*** (2.99) | 1.256*** (3.04) |
| Other retinal disorder | 0.0492*** (-12.32) | 0.0490*** (-12.33) | 0.0590*** (-11.19) | 0.0573*** (-11.29) |
| Congenital Heart Disease | 0.622*** (-8.40) | 0.615*** (-8.56) | 0.669*** (-6.25) | 0.656*** (-6.48) |
| Necrotizing enterocolitis in fetus or infant | 0.743*** (-2.64) | 0.734*** (-2.74) | 0.826 (-1.51) | 0.813 (-1.63) |
| Total number of beds | 1.001*** (2.60) | 1.001 (0.57) | ||
| Number of acute infant intensive care beds | 0.998** (-2.08) | 0.998** (-2.54) | ||
| LR chi2 | 3112 | 3109.6 | 2219.3 | 2225.5 |
| Prob>chi2 | 0 | 0 | 0 | 0 |
| Observations | 9593 | 9593 | 6732 | 6732 |
The Cox proportional hazard model involves alterations in the settings of the dependent variable, which is based on sudden decreases in the mortality rate. The results for the basic model (without the disease control variables) are presented in Table 4, the basic model with the disease control variables is presented in Table 5, the basic model and the number of hospital beds is presented in Table 6, and the basic model with the disease control variables and the number of hospital beds is presented in Table 7 The empirical results are presented for the mixed and paper card samples. The difference between the mixed and paper card samples is that the paper card sample has an additional infant gender variable.
With regard to the setting of the infant experience variable, this paper uses the number of infants treated over a given period as infant experience. There is no significant difference in the results after infant experience reaches five years, such that the first five years are significant but not thereafter. Hence, in reporting the empirical results, the physician’s and hospital infant experience both refer to infant experience over a period of five years.
The definition and determination of experience in treating infants by both a physician and a hospital, hereafter termed “physician’s experience” and “hospital experience”, respectively, can be problematic. Virtually all previous studies in the literature have used one year of data, and hence have defined infant experience as the number of infants treated by a physician or a hospital during the same year. Such a definition of contemporaneous experience is severely restricted. The data set in this paper allows “experience” to be defined for up to 13 years. There is a balance required between increasing the number of years of infant experience and the concomitant loss of an equivalent number of years from the sample set. Preliminary empirical analysis showed that 2, 3, 4 and 5 years of infant experience were preferred statistically to a single year of experience, but that 6 years of infant experience was not statistically superior to 5 years. In the interests of a parsimonious balance between a practical and realistic measure of infant experience and the substantial loss of data in defining such infant experience, this paper defines both a physician’s and also a hospital’s infant experience as based on 5 years of treatment of infants.
Table 4 shows the empirical results for the basic model, with the second column giving the mixed sample estimates and the third column giving the paper card estimates. The mixed sample estimates show that the heavier is the infant’s weight, the higher is the significant drop in the sudden mortality rate. For example, the sudden infant mortality rate for weights between 1250 g and 1499 g is 0.0285 times that of weights below 500 g. This result is consistent with the empirical findings in Cifuentes [11], Wung [14] and Phibbs [15]. The physician’s gender as male is insignificant, but the physician’s seniority and age are significant, with seniority lowering the sudden mortality rate, and age increasing the sudden mortality rate.
For hospital characteristics, only the medical center is significant, whereby the sudden mortality rate of an infant living in the medical center is 0.75 times that of an infant not living in the medical center. The infant experience of a physician and hospital are significant, with a hazard ratio of 0.999, which represents a decrease of 0.1% in the sudden mortality rate for each increase in infant experience.
The third column in Table 4 gives the paper card estimates results, wherein sudden infant mortality rate for weights between 1250 g and 1499 g is 0.0244 times that of weights less than 500 g. For male infants, the sudden mortality rate is 1.406 times that of female infants, which is consistent with the empirical findings in Cifuentes [11], Rogowski [12], and Phibbs [15]. A physician’s seniority (increase in experience) can decrease the sudden mortality rate, while an increase in the physician’s age (physical decline) can increase the sudden mortality rate. Infants living in the medical center can significantly decrease the sudden mortality rate, which is 0.71 times that of not living in the medical center. The infant experience of physicians and hospital is significant, with a hazard ratio about 0.999, which represents a decrease of 0.1% in the sudden mortality rate for each additional infant. The hospital infant experience and mortality rate have a significant negative relationship, which is consistent with the empirical findings in Phibbs [10], Rogowski [12], Bartels [13], and Phibbs [15].
Table 5 gives the empirical results for the basic model with the disease control variables in the second column for the mixed sample estimates, and in the third column for the paper card estimates. After adding the disease control variables, the mixed sample estimates show that a higher infant weight can significantly decrease the sudden mortality rate: for example, the sudden mortality rate for weights between 1250 g and 1499 g is 0.0294 times that of weights less than 500 g. Infants treated by a male physician can significantly increase the sudden mortality rate, which is 1.082 times that of infants treated by a female physician. The effect of a physician’s seniority (increase in experience) and age (physical decline) on the mortality rate is statistically significant and negative.
Infants living in the medical center can significantly decrease the sudden mortality rate, which is 0.87 times that of infants not living in the medical center. Staying in the medical center of public hospitals can also significantly lower the sudden mortality rate, which is 0.875 times that of infants staying in a non-medical center and non-public hospital. The effect of physicians with infant experience becomes insignificant, and a hospital with infant experience significantly lowers the sudden mortality rate by 0.1% for each additional infant.
The third column in Table 5 gives the paper card estimates with the disease control variables. A heavier infant’s weight can significantly lower the sudden mortality rate, and a male infant can significantly increase the sudden mortality rate to 1.339 times that of a female infant. Treatment of an infant by a male physician can significantly increase the sudden mortality rate, which is 1,137 times that of an infant treated by a female physician. A physician’s seniority significantly lowers the sudden infant rate, but the physician’s age is insignificant. An infant living in a medical center can significantly lower the sudden mortality rate, which is 0.811 times that of a infant not living in a medical center. Staying in the medical center of a public hospital can also significantly lower the sudden mortality rate, which is 0.858 times that of an infant staying in a non-medical center and nonpublic hospital. A physician’s experience becomes insignificant, but a hospital’s experience can significantly lower the sudden mortality rate by 0.1% for a unit increase in infant experience.
Table 6 uses the basic model and the hospital bed control variable to examine whether the addition of a disease control variables cause the physician’s and hospital infant experience to become insignificant. The second and third columns show the estimates of the mixed sample, while the fourth and fifth columns show the estimates of the paper card sample. All the mixed sample results are similar for the total number of hospital beds and the acute infant intensive care beds, as follows: a heavier infant’s weight can significantly reduce the sudden mortality rate; a physician’s seniority and age are significant and negative; staying in a medical center can significantly reduce the sudden mortality rate; and a physician’s infant experience, physician’s gender, and the hospital bed control variable are not significant; and the hospital infant experience can significantly reduce the sudden mortality rate at the 10% level of significance.
The results in the fourth and fifth columns in Table 6 for the paper cards sample show the common points for the total number of hospital beds and acute infant intensive care beds, as follows: the heavier is the infant’s weight, the lower is the sudden mortality rate; a male infant significantly increases the sudden mortality rate, a male physician significantly increases the sudden mortality rate, and a medical center significantly lowers the sudden mortality rate. A physician’s and hospital’s infant experience, and the hospital bed variable, are not significant, and a physician’s seniority and age are also insignificant.
Table 7 provides the empirical results of the basic model, and control for the disease variables and number of hospital beds. The second and third columns show the estimates of the mixed sample, while the fourth and fifth columns give the estimates of the paper cards. Both the mixed and paper samples show that, regardless of the total number of hospital beds or acute infant intensive care beds as the control variable, the infant experience of both physicians and hospitals become insignificant.
The mixed sample total hospital beds variable gives the results of hospital beds as a control, as shown in the second column. A heavier infant’s weight can significantly reduce the sudden mortality rate: for example, the sudden mortality rate for an infant’s weight between 1250 g and 1499 g is 0.0277 times that of a weight of less than 500 g. A male physician can significantly increase the sudden mortality rate, which is 1.132 times that of a female physician. Both a physician’s seniority and age are significant, but the former (increase in experience) can reduce the sudden mortality rate while the latter (physical decline) can increase the sudden mortality rate. Moreover, the sudden mortality rate of staying in the medical center is 0.649 times that of staying in a non-medical center.
The mixed sample results for acute infant intensive care beds are based on the hospital bed control variable, and are shown in the third column. The sudden mortality rate of infant’s weights between 1250 g and 1499 g is 0.0276 times that of weights less than 500 g; the sudden mortality rate for a male physician is 1.092 times that of a female physician; both a physician’s seniority and age are significant and negative; and the sudden mortality rate of staying in a medical center is 0.677 times that of staying in a non-medical center.
The difference between the second and third columns of the mixed sample estimates is the total number of hospital beds, which can significantly increase the sudden mortality rate; acute infant intensive care beds can significantly reduce the sudden mortality rate; and the sudden mortality rate can be lowered by 0.2% with each increase in acute infant intensive care beds.
The total number of hospital beds results for the paper card sample are based on the hospital beds control variable, and are shown in the fourth column. A heavier infant’s weight can significantly reduce the sudden mortality rate: for example, the sudden mortality rate of infant’s weights between 1250 g and 1499 g is 0.0273 times that of weights less than 500 g. A male infant can significantly increase the sudden mortality rate, which is 1.357 times that of a female infant. A male physician can significantly increase the sudden mortality rate, which is 1.175 times that of a female physician. An infant staying in a medical center can significantly lower the sudden mortality rate, which is 0.689 times that of staying in a non-medical center. The physician’s age is not significant.
The results for the paper card sample acute infant intensive care beds rely on the hospital beds control variable, and are shown in the fifth column. The sudden mortality rate of an infant’s weight between 1250 g and 1499 g is 0.0272 times that of a weight less than 500 g. A male infant can significantly increase the sudden mortality rate, which is 1.357 times that of a female infant. The sudden mortality rate of an infant treated by a male physician is 1.149 times that of a female physician. A physician’s seniority and age are not significant. The sudden mortality rate of staying in a medical center is 0.709 times that of staying in a non-medical center.
For the estimates of the paper card sample with the addition of the hospital bed control variable, the total number of hospital beds is not significant. The acute infant intensive care beds can significantly reduce the sudden mortality rate by 0.2% for each acute newborn intensive care bed.
An infant staying in a medical center (higher hospital evaluation classification) and a hospital’s investment increase in neonatology (measured as the number of acute infant intensive care beds) both reduce the sudden mortality rate, which is consistent with the empirical findings in Phibbs [10], Cifuentes [11] and Phibbs [15].
These empirical results show that, in a model with disease control variables but excluding a hospital bed variable, the hospital experience can explain the medical care quality for minimal birth weight infants, but the physician’s infant experience cannot do so. With both the disease control variables and hospital bed variable in the model, neither a physician’s infant experience nor hospital infant experience has explanatory power. Using acute infant intensive care beds to capture investment in neonatology, the greater is the investment, the better is the medical care quality for minimal birth weight infants.
For the basic model with control for disease and hospital beds, regardless of a mixed sample or a paper card sample, the acute infant intensive care beds can significantly reduce the sudden mortality rate. The hospital evaluation classification means that the medical center and the sudden mortality rate have a negative relationship, and the medical center has useful explanatory power for the sudden mortality rate of minimal birth weight infants. In short, the medical center is, not surprisingly, a critical factor in measuring medical quality.
Conclusion
This paper used data for minimal birth weight infants from 1997 to 2009 in the Taiwan National Health Insurance database as the research subjects, and the Cox proportional hazard model to conduct an empirical analysis on the sudden mortality rate of minimal birth weight infants hospitalized for the first time. The main explanatory variables included the physician’s and hospital infant experience, the physician’s gender, seniority and age, the hospital’s evaluation classification and ownership, and the number of hospital beds.
As discussed above, prior to September 2003, the Taiwan National Health Insurance scheme used paper cards and did not allow infants to access their mothers’ health insurance for medical services. However, after September 2003, the National Health Insurance scheme switched to IC cards so that, within the first 31 days of birth, infant could access their mother’s health insurance IC cards for medical treatment. This paper showed the empirical analysis of paper card and mixed sample (that is, paper and IC cards), and provided the paper card effects of the infant gender variable.
In summary, the main conclusions of the empirical analysis are as follows:
Infant characteristics: increases in weight classification can steadily and significantly lower the sudden mortality rate, and male infants have higher sudden mortality rates than do female infants.
Physician characteristics: physicians with infant experience have a negative correlation with the sudden mortality rate for the basic model with no control variable. In contrast, physicians with infant experience have no significant effect if diseases and the number of hospital beds are subject to control. In all the estimates for the mixed samples, a physician’s seniority (or increase in experience) and age (physical decline) are both significant, and have negative effects on the sudden mortality rate. In the mixed sample, under disease control, male physicians can increase the sudden mortality rate. Incorporation of the disease control variables and the number of hospital beds in the paper card sample can significantly increase the sudden mortality rate for male physicians.
Hospital characteristics: hospitals with infant experience have a negative relationship with the sudden mortality rate, and an increase in acute infant intensive care beds can significantly lower the sudden mortality rate for the basic model with control for the disease variable. Hospital infant experience does not significantly lower the sudden mortality rate if both the disease and the number of hospital beds are controlled. The medical center and the sudden mortality rate have a significant negative relationship.
There are important issues in sample selection (Figure 1). Although the empirical results show that the evaluation classification means that the medical center represents higher medical care and/or higher infant experience for neonatology, the medical center has a lower sudden mortality rate compared with hospitals with other evaluation classifications (Figure 1).
This paper excludes all referral infants, but has no control over the mother’s referral, the mother’s past medical history, and related socio-economic variables, for which data are not available. Based on Wang [17], using maternal and neonatal research subjects in Taiwan in 2001, the estimation results by quantile regression show that the mother’s past medical history, weeks of pregnancy, and age can affect infant weights. The studies by Phibbs [10], Cifuentes [11], Rogowski [12], and Phibbs [15] have examined the mother’s socio-economic status to control the effects of social and economic variables.
Restricted by the nature of the available data, the fact that not every infant has insurance under their mothers’ name, the Taiwan National Health Insurance database is unable to connect newborns to their mothers’ data, despite the insurance data files containing such information. In order to protect privacy, the National Health Insurance database does not allow linkages from external sites, so it is not possible to obtain information that is related to the maternal socio-economic status.
In all the models based on the paper card samples, minimal birth weight male infants significantly increase the sudden mortality rate. However, due to the adoption of IC cards by the National Health Insurance scheme from September 2003, it is not possible to determine gender from infants seeking medical treatment under their mothers’ insurance policies.
Controlling an infant’s disease severity is based on the detailed hospitalization expense file records that describe the disease with a clinical diagnosis of the disease severity. Warner et al. (2004) incorporated the clinical disease severity and showed that the estimates may change quantitatively, but that such inclusion will not likely change the qualitative conclusions. Incorporating the disease control variables in the mixed sample, or incorporating the disease control variables and/or number of hospital beds in the paper cards sample, makes the male physician variable significantly increase the sudden infant mortality rate.
This paper lacks information on the mother’s past medical history, socio-economic variable, infant gender, disease clinical severity, and how physicians are assigned to minimal weight infants, all of which might affect the empirical estimates. The limitations of the database are dependent on how the data are stored and linked in the Taiwan National Health Insurance scheme. The addition of an infant’s disease clinical severity and information regarding internal hospital resource assignments for infants, providing greater in-depth studies based on related medical resource usage, and medical quality for minimal birth weight infants, would enable greater precision in analyzing the sudden infant mortality rate.
Acknowledgement
The authors are most grateful to a reviewer for very helpful comments and suggestions, and wish to thank the Taiwan National Health Research Institutes for providing the data, and the National Science Council, Taiwan for financial support. The third author also wishes to acknowledge the Australian Research Council.
1 https://w3.nhri.org.tw/nhird//faq_e.htm
2https://www.nhi.gov.tw/webdata/webdata.aspx?menu=20&menu_ id=710&WD_ID=710&webdata_id=3638
3http://www.nhi.gov.tw/webdata/webdata.aspx?menu=20&menu_ id=710&WD_ID=811&webdata_id=3638
4https://www.nhi.gov.tw/webdata/webdata.aspx?menu=6&menu_ id=817&WD_ID=198&webdata_id=2678
References
- Buehler JW, Hogue CJR, Zaro SM (1985) Postponing or Preventing Deaths? Trends in Infant Survival, Georgia, 1974 through 1981. Journal of the American Medical Association 253: 3564-3567.
- Goodman DC, Fisher ES, Little GA, Stukel TA, Chang CH (2001) Are Neonatal Intensive Care Resources Located According to Need? Regional Variation in Neonatologists, Beds, and Low Birth Weight Newborns. Pediatrics 108: 426-431.
- Warner B, Musial MJ, Chenier T, Donovan E (2004) The Effect of Birth Hospital Type on the Outcome of Very Low Birth Weight Infants. Pediatrics 113: 35-41.
- Gaynor M,Seider H, Vogt WB (2005) The Volume-Outcome Effect, Scale Economies, and Learning-by-Doing. American Economic Review 95: 243-247.
- Sfekas A (2009) Learning, Forgetting, and Hospital Quality: An Empirical Analysis of Cardiac Procedures in Maryland and Arizona. Health Economics 18: 697-711.
- Hsu PF (2009) The Volume-Outcome Relationships in Coronary Artery Bypass Graft Surgery. Taiwan Journal of Public Health 28: 69-77.
- Hockenberry JM, Lien HM, Chou SY (2010) Surgeon and Hospital Volume as Quality Indicators for CABG in Taiwan:Examing Hazard to Mortality and Accounting for Unobserved Heterogeneity. Health Services Research, 45: 1168-1187.
- Chien LN, Chu HF, Liu CH, Chung KP, Tsauo JY, et al. (2003) Association Between Hospital and Surgeon Procedure Volume With Outcome of Total Hip Replacement.Taiwan Journal of Public Health 22: 118-126.
- Holmstrom ST,Phibbs CS (2009) Regionalization and Mortality in Neonatal Intensive Care. Pediatric Clinics of North America 56: 617-630.
- Phibbs CS, Bronstein JM, Buxton E, Phibbs RH (1996) The effect of Patient Volume and Level of Care at the Hospital of Birth on Neonatal Mortality. Journal of the American Medical Association 276: 1054-1059.
- Cifuentes J, Bronstein J, Phibbs CS, Phibbs RH, Schmitt SK, et al. (2002) Mortality in Low Birth Weight Infants According to Level of Neonatal Care at Hospital of Birth. Pediatrics 109: 745-751.
- Rogowski JA, Horbar JD, Staiger DO, Kenny M, Ceppert J (2004) Indirect vs Direct Hospital Quality Indicators for Very Low-Birth-Weight Infants. Journal of the American Medical Association 291: 202-209.
- Bartels DB, Wypij D, Wenzlaff P, Dammann O, Poets CF (2006) Hospital Volume and Neonatal Mortality Among Very Low Birth Weight Infants. Pediatrics 117: 2206-2214.
- Wung SH, Huang YT, Yang CH, Lu TH (2005) An Empirical Evidence Study between Physician Volume and Quality of Care in Very Low Birth Weight Infants. Formosan Journal of Medicine 9: 448-454.
- Phibbs CS, Baker LC, Caughey AB, Danielsen B, Schmitt SK, et al. (2007) Level and Volume of Neonatal Intensive Care and Mortality in Very-Low-Birth-Weight Infants. The New England Journal of Medicine 356: 2165-2175.
- Hosmer DW, LemeshowS, May S (2008) Applied Survival Analysis: Regression Modeling of Time to Event Data, Wiley, New York.
- Wang SM, Kuan CM, Lo JC (2006) The Effects of Maternal Characteristics and Pregnancy Status on Birth Weights. Taiwan Journal of Public Health 25: 478-481.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences