Journal of Health & Medical Economics

Introduction

In this editorial, Alghalith provide a summary of selected recent articles that can be applied to the investment in the stocks of medical corporations.

Alghalith [1] overcame a significant obstacle in the existing literature on forward dynamic utilities and related investment models. In doing so, it established the existence and uniqueness of the solutions and it showed that the assumptions needed for these solutions are similar to the solutions using a backward dynamic utility function. Moreover, it applied Hausdorffcontinuous viscosity solutions to financial modelling. According to Alghalith [1], the forward dynamic utility is given by

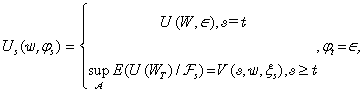
where U is the utility function and V is the value function; the form of the utility is determined by the stochastic variable ?. Alghalith [2] introduced a new stochastic factor (portfolio) model. In doing so, it provided an explicit solution to the portfolio model. More-over, it showed that the optimal portfolio does not depend on the investor’s preferences.

Alghalith [3] considered a portfolio model with an unknown investment horizon. It derived solutions to the optimal portfolio without adding significant complexities to the standard model (the model with known horizon).

Similarly, Alghalith [4] relaxed the assumption of self-financing strategies. This was done without a significant complication of the optimal solutions.

Alghalith [5] provided classical solutions to the portfolio optimization problem under a non-differentiable value function. Therefore, it did not rely on the traditional approaches such as the HJB PDEs and viscosity solutions.

In sum, this opinion Article highlights the interface between mathematical finance and health economics.

References

1. Alghalith M (2012) Forward dynamic utility functions: A new model and new results. European Journal of Operational Research 223: 842-845.
2. Alghalith M (2009) A new stochastic factor model: general explicit solutions. Applied Mathematics Letters 22: 1852-1854.
3. Alghalith M (2012) Optimal Portfolio Control with Unknown Horizon. Journal of Mathematical Finance 2: 41-42.
4. Alghalith M (2011) Portfolio Optimization without the Self-Financing Assumption. Advances in Pure Mathematics 1: 81-83.
5. Alghalith M (2012) New solutions for non-smooth value functions. Comptes rendusmathématiques de l’Académie des sciences 34: 1-4.